How to Use Solver in Excel (2 Practical Examples)

Sometimes you need to make the most of what you have, like limited time, money, or materials. Solver in Excel helps you do just that. It finds the best solution by changing certain values while following the rules you set. In this guide, we will show you how to use Solver with two real examples: one for deciding how many products to make with limited resources, and another for planning a budget without spending too much.

What is Solver in Excel and How Does It Work?

Solver is a built-in Excel tool that helps you find the best answer by changing some values while following certain criteria. It is useful when you want to do calculations like maximizing profit, staying under budget, or planning with limited resources.

To get started with Solver:

• Turn it on: Go to File > Options > Add-ins, click Go, checkmark Solver Add-in, and hit OK.
• Set your goal: Choose the cell you want to improve (like total profit) and tell Excel whether to make it as big, small, or exact value as you want.
• Pick the cells Solver can change: These are the values Excel will adjust to reach your goal.
• Add rules (constraints): For example, you can tell Solver not to go over a certain number or to use whole numbers only.
• Click Solve: Excel will try different options and give you the best result based on your setup.

2 Examples of Using Solver in Excel

In this article, we will show you how to use Solver in Excel through two practical examples: optimizing production with limited labor and materials, and allocating a school renovation budget without exceeding set limits.

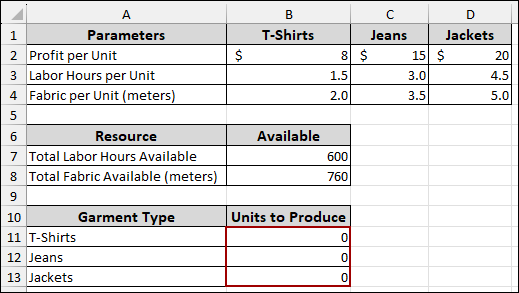
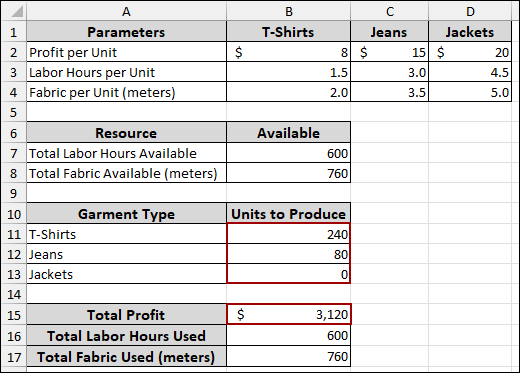
Suppose we have a dataset containing the Profit per Unit, Labor Hours per Unit, and Fabric per Unit for three garment types: T-shirts, Jeans, and Jackets. We also have the Total Labor Hours Available and Total Fabric Available (meters) as our constraints. Below we have the Garment Type and Units to Produce, where we will get the values that can be produced according to the parameters and resources.

This means we can only produce as many T-shirts, Jeans, and Jackets according to our available labor hours and fabric. Here, Solver will confirm that the total hours and fabric used for production do not go beyond these limits while trying to maximize the total profit.

Example 1: Optimizing Production with Limited Resources

Starting with, we will calculate the Total Profit, Total Labor Hours Used, and Total Fabric Used. Then, we will use the Solver to find the optimal production units with our provided resources.

➤ First, insert 0 in (cell B11, B12, B13) in all the Units to Produce section for T-shirts, Jeans, and Jackets.

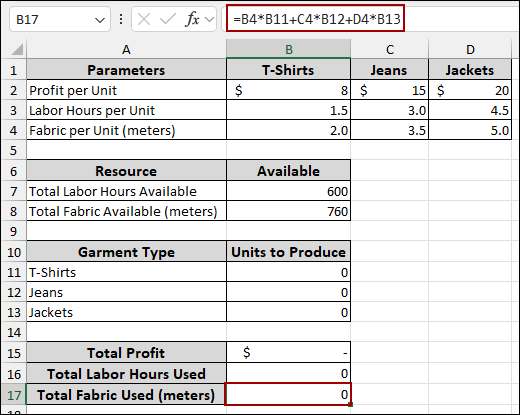
➤ Choose cell B15 and input the formula below.

This formula calculates the Total Profit by multiplying the Profit per Unit for each garment type (B2, C2, D2) by the corresponding Units to Produce (B11, B12, B13) and summing the results.

➤ Select cell B16 and write down the following formula.

➤ Select cell B17 and put the following formula.

To begin the Solver process and find the optimal production:

➤ Click on the Data tab from the menu bar.
➤ In the Analyze group, click on Solver.

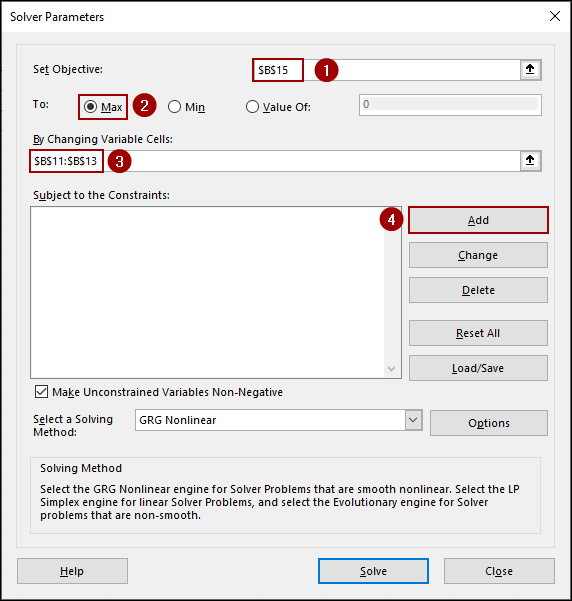
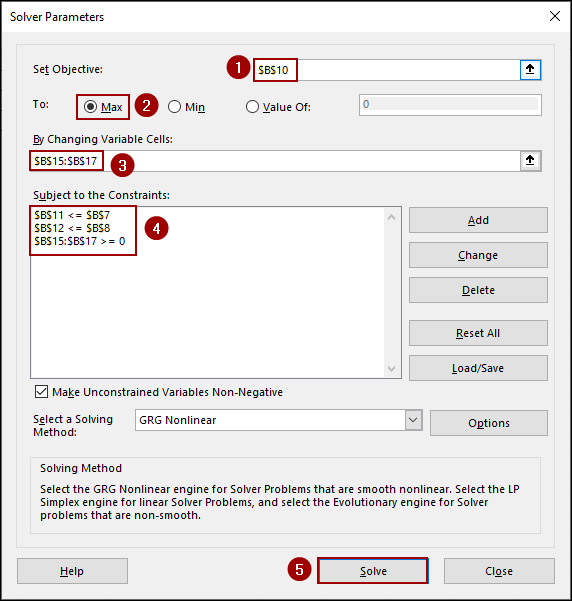
In the Solver Parameters dialog box, we will define the objective, the variable cells, and the constraints.

➤ In the Set Objective field, enter B15, as this is the cell containing the formula for our Total Profit.
➤ Choose the Max option to maximize the total profit.
➤ In the By Changing Variable Cells field, select B11:B13, as these are the cells containing the units of each product we want Solver to adjust.
➤ Click the Add button to add constraints in the Subject to the Constraints field.

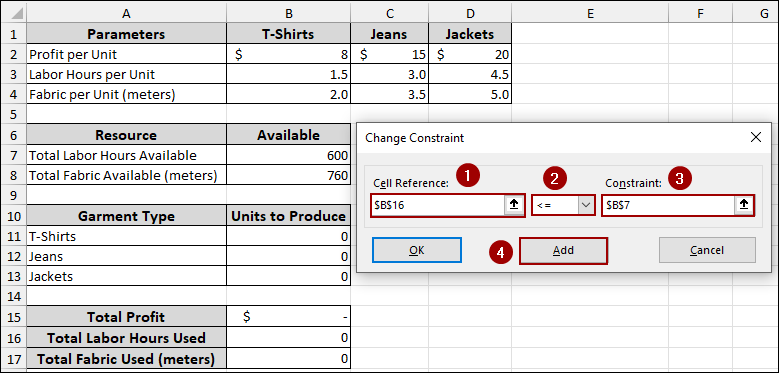
➤ To add our first constraint, choose B16 in the Cell Reference field.
➤ From the dropdown menu, select <=.
➤ In the Constraint field, put B7, which is our Total Labor Hours Available.
➤ Click Add.

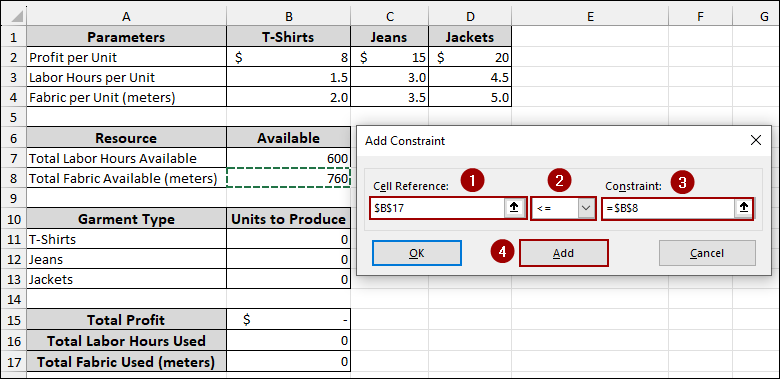
➤ In the new constraint window, enter B17 in the Cell Reference field.
➤ Select <= from the dropdown menu.
➤ In the Constraint field, choose B8, which is our Total Fabric Available.
➤ Hit Add.

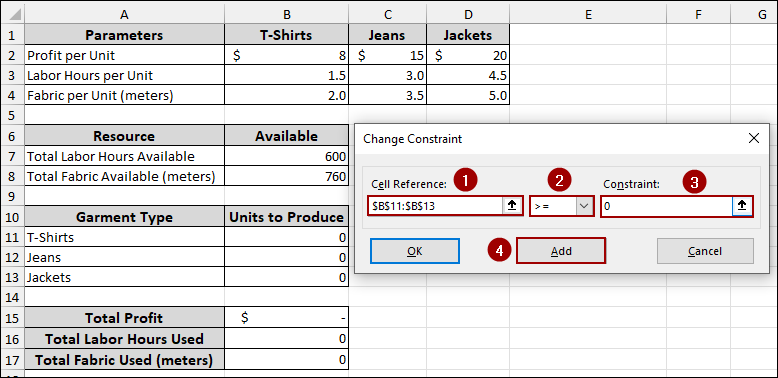
To ensure that the units produced are non-negative, add one more constraint.

➤ Choose cell range B11:B13 in the Cell Reference field.
➤ Select >= from the dropdown menu.
➤ Input 0 in the Constraint field.
➤ Press OK.

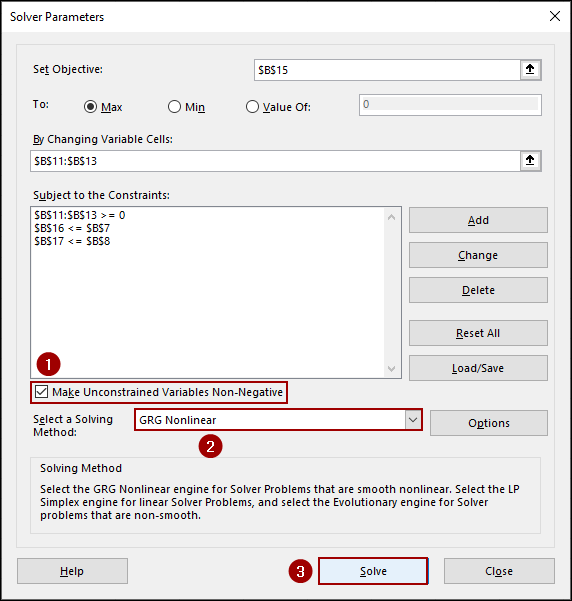
After defining all the constraints, you will see them listed in the Solver Parameters dialog box.

➤ Now, checkmark the box for Make Unconstrained Variables Non-Negative.
➤ From the Select a Solving Method dropdown menu, choose GRG Nonlinear.
➤ Finally, click Solve.

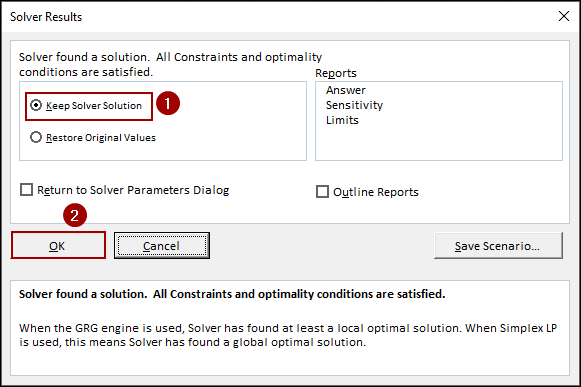
After clicking Solve, the Solver Results dialog box will appear.

➤ Choose Keep Solver Solution and press OK.

As a result, the values in cells B11 to B13 will change to 240 T-shirts, 80 Jeans, and 0 Jackets. This indicates that producing this combination of garments will yield the maximum total profit of $3,120 while utilizing all available labor hours and fabric.

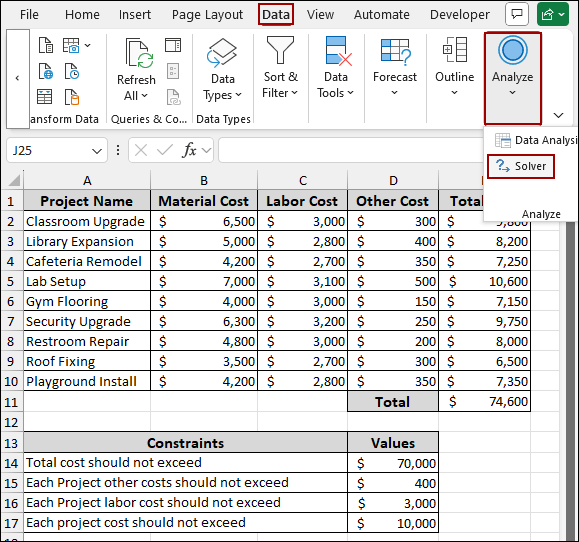
Example 2: Allocating Budget Without Going Over the Limit

In this example, we will show you how to use Solver to find a new set of project costs that meet specific budget constraints.

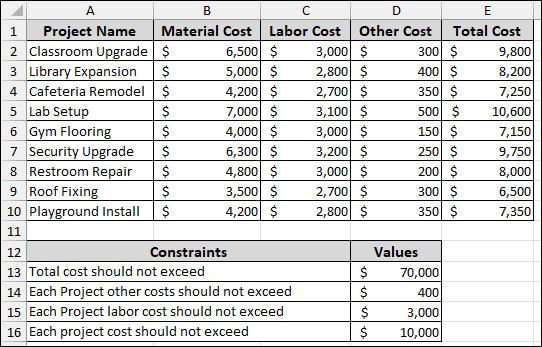
Imagine we have a list of ten projects with their respective costs and constraints. Now, we will use Solver to adjust the costs of each project so that the total cost does not exceed $70,000, while also meeting other individual project constraints.

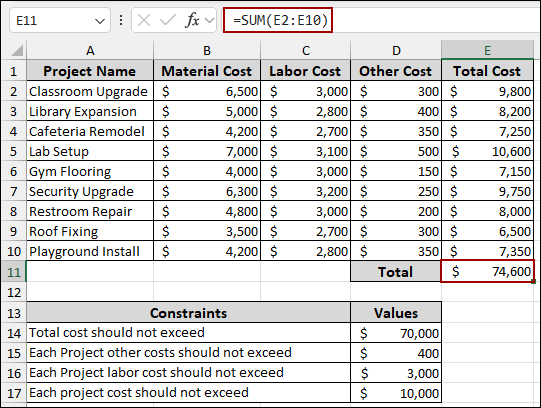
First, we will calculate the Total Cost of all the projects using the SUM function.

➤ Choose cell E11 and input the following formula.

To begin the Solver process and find a solution that meets the budget:

➤ Click on Data > Analyze > Solver.

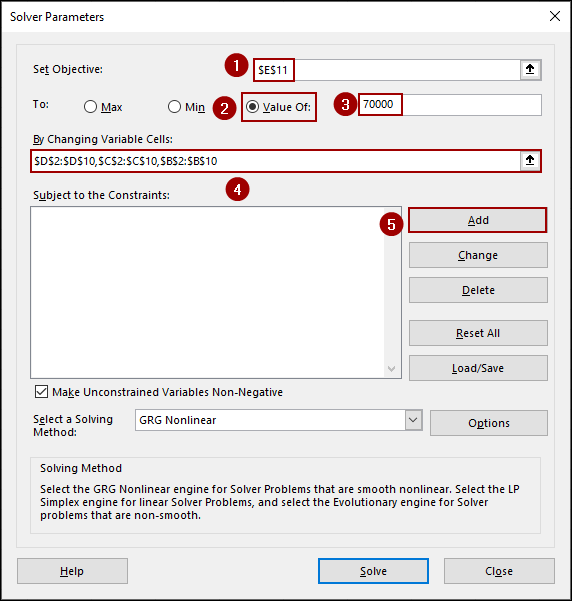
In the Solver Parameters dialog box, we will define the objective, the variable cells, and the constraints.

➤ In the Set Objective field, enter E11, as this is the cell containing the formula for our Total Cost.
➤ Choose the Value Of option and enter 70000, which is our desired total cost.
➤ In the By Changing Variable Cells field, enter B2:B10, C2:C10, D2:D10, as these are the cells containing the Material, Labor, and Other Costs that Solver should adjust.
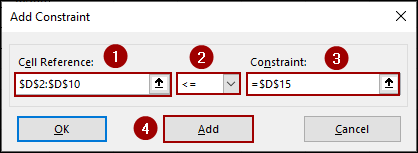
➤ Click the Add button in the Subject to the Constraints section.

➤ In the Cell Reference field, enter D2:D10.
➤ From the dropdown menu, select <=.
➤ In the Constraint field, enter D15, which is our Each Project other costs should not exceed value.
➤ Click Add.

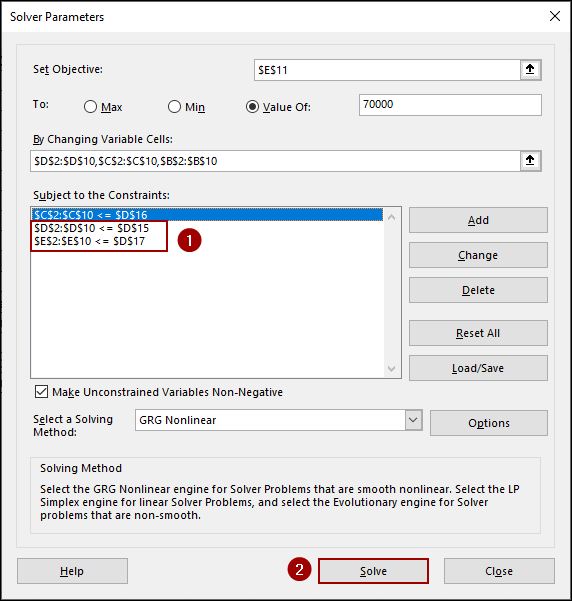
➤ Similarly, we will add some more constraints:

C2:C10 <= D16
E2:E10 <= D17

➤ Finally, click Solve.

As a result, the values for Material Cost, Labor Cost, and Other Cost for each project will change. The total cost in cell E11 will also be exactly $70,000, indicating that the new costs for all projects meet the desired budget while staying within the specified constraints.

Frequently Asked Questions

Where can I find Solver in Excel?

Go to the Data tab and look for Solver on the right. If you don’t see it, you will need to enable it by going to: File > Options > Add-ins > Excel Add-ins > Go, then checkmark Solver Add-in and click OK.

What’s the difference between Solver and Goal Seek?

Goal Seek changes one input to reach a target output. Solver, on the other hand, can change multiple inputs while considering constraints, making it more versatile for complex scenarios.

Is there a limit to the number of variables or constraints Solver can handle?

Yes, in standard Excel, Solver has limits (200 decision variables for GRG Nonlinear), but you can upgrade to Solver Premium from Frontline Systems for larger models.

Concluding Words

Above, we have explored how to use Solver in Excel to find the best possible solution while staying within set limits. Whether you’re optimizing production with limited resources or allocating a budget across multiple projects, Solver helps you find the most effective solution based on your goals and constraints. If you have any questions, feel free to leave them in the comments below.