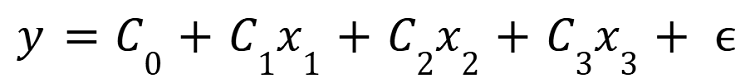Multiple linear regression is a useful tool for estimating a dependent variable’s value based on a number of independent variables. Excel makes it simple to carry out regression analysis, whether you’re predicting sales, studying consumer behavior, or projecting home prices. This article explores what multiple linear regression is and how to do multiple linear regression in Excel using built in tools and functions. Additionally, the regression analysis results will be discussed in detail.
➤ Multiple linear regression models the relationship between one dependent variable and multiple independent variables. In this article, we’ll learn about multiple linear regression and how to do multiple linear regression in Excel using Data Analysis ToolPak and the LINEST function.
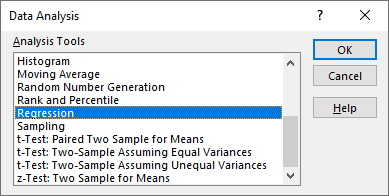
➤ Enable Data Analysis: File >> Options >> Excel Add-ins >> Data Analysis.
➤ Regression: Data tab >> Data Analysis >> Regression >> Input Y range >> Input X ranges >> Labels >> Output range >> OK.
➤ LINEST function: =LINEST(known_ys,[known_xs],[const],[stats])
What Is Multiple Linear Regression?
Multiple linear regression models the relationship between one dependent variable (outcome) and two or more independent variables (predictors).
It is essentially an extension of simple linear regression that includes multiple independent variables. Rather than fitting a single line, the model uses the least squares approach to fit a surface that minimizes the total distance or error between the actual and predicted values.
The general equation for multiple linear regression is:
where,
- y is the dependent variable
- x1,x2,x3 are the independent variables
- C1,C2,C3 are the coefficients that shows the change in y for each unit change in x
- C0 is the y intercept or the point where the regression line crosses the y axis
- ∊ is the error term representing the difference between the actual and predicted values.
There is always an error between the actual and predicted values. This is represented by the error term (∊). Excel accounts for this error while determining the coefficients (C₀, C₁, C₂, C₃) for the line of best fit
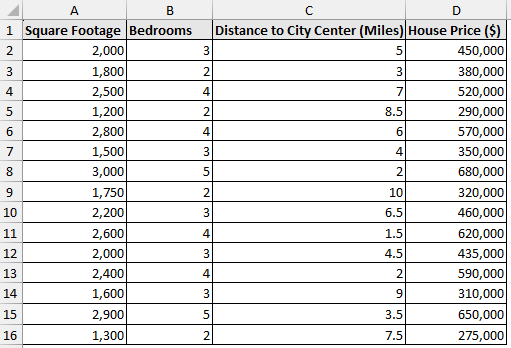
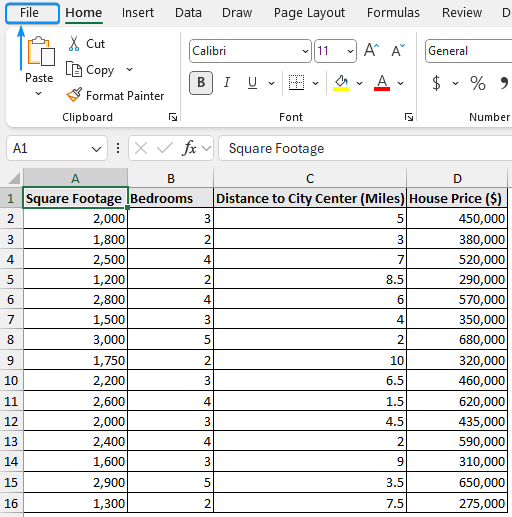
Continuing with our real estate analyst example, you want to predict house prices based on several variables such as square footage, number of bedrooms, and distance to the city center. The house price is the dependent variable (outcome). The square footage, bedrooms, and distance are the independent variables (predictors).
By performing multiple linear regression, you can quantify the relationship between these variables through an equation.
This multiple linear regression model helps predict house prices more accurately by considering several variables simultaneously. There are two ways to perform multiple linear regression in Excel using the Data Analysis ToolPak and the LINEST function. Let’s explore each in detail.
Multiple Linear Regression in Excel with Data Analysis ToolPak
Excel’s Data Analysis ToolPak is a built in software to perform multiple regression. It’s easy to use and offers comprehensive statistical results, such as p values, R squared, etc., which help determine the independent variables that have a significant impact on the dependent variable. To use this tool, we need to activate it first.
Steps:
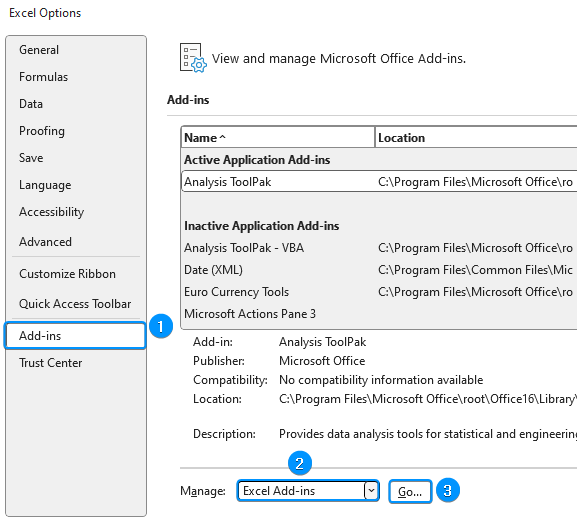
➤ Click on the File tab.
➤ Select Options. You can also use the shortcut Alt + F + T to open Excel Options.
➤ Select Add-ins >> Choose Excel Add-ins from the dropdown >> Go.
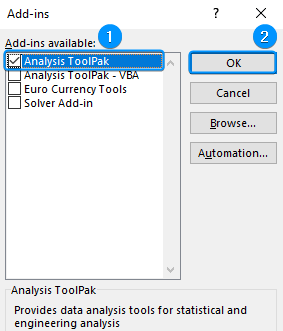
➤ Check the Analysis ToolPak option >> OK
.
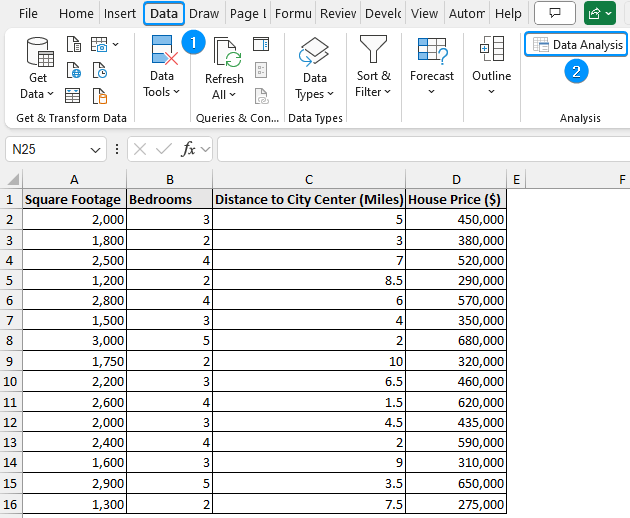
The Data Analysis ToolPak will be available in the Data tab whenever you open a new workbook.
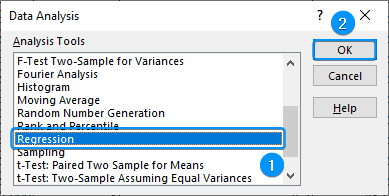
➤ Go to the Data tab >> Click Data Analysis.
➤ Select Regression >> OK.
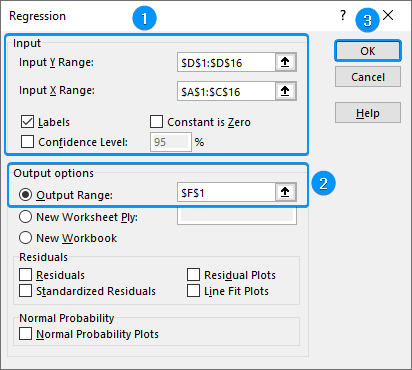
➤ Select Input Y Range (D1:D16) and Input X Range (A1:C16).
➤ Check the Labels option >> Output Range (F1) >> OK.
Interpretation of Multiple Linear Regression Results
The simple linear regression post discusses the regression statistics and ANOVA tables in detail. Let’s now examine some key metrics.
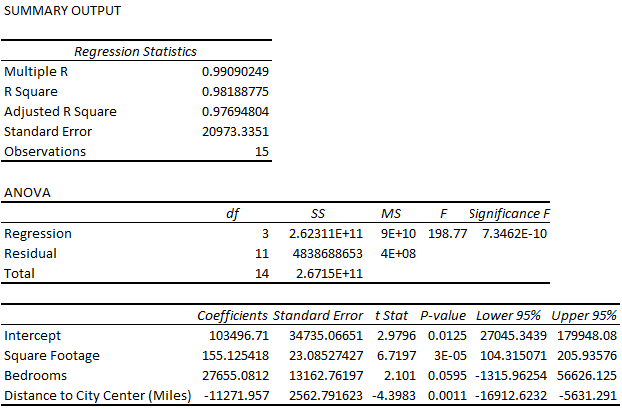
➥ R Square: The coefficient of determination measures the proportion of variance in the dependent variable that is explained by the independent variable. In this case, 98.2% of the variation in house prices can be explained by the square footage, number of bedrooms, and distance to the city center variables.
➥ Standard Error: The average distance the observations are located from the regression line. For example, on average, the observed values are located 20,973.3 units from the regression line.
➥ F statistic: The F statistic can be found by dividing the regression MS by the residual MS.
➥ Significance F: The P value of the F statistic. The significance F reveals if the three independent variables have a significant relationship with the dependent variable. For example, the P value is less than the significance level (0.05), confirming that square footage, number of bedrooms, and distance to the city center significantly impact the house price.
➥ P values: The P value for each independent variable reveals its statistical significance. For instance, the square footage (0.00003) and distance to city center (0.0011) are significant while the number of bedrooms (0.0595) is not significant so we may remove this variable from our model.
➥ Coefficients: The coefficients for each independent variable represent the average change in the dependent variable, assuming other independent variables remain constant. For example, the house price increased by $155.13 for each unit increase in the square footage. Again, each unit increase in the distance to city center caused the house price to decrease by $11,271.96.
Replacing the values from the regression output:
House price = 103,496.71 + 155.13 * Square footage + 27,655.08 * Bedrooms - 11,271.96 * Distance to city center
Plug the square footage, bedrooms, and distance to city center values to calculate the house price based on the regression model.
Using LINEST Function for Multiple Linear Regression in Excel
While the Data Analysis ToolPak offers a detailed summary, the LINEST function allows you to carry out multiple linear regression quickly. However, one drawback is that it returns the results as an array, making it hard to tell which value represents which statistic. In this section, we will show the steps and reveal each value in the array.
Steps:
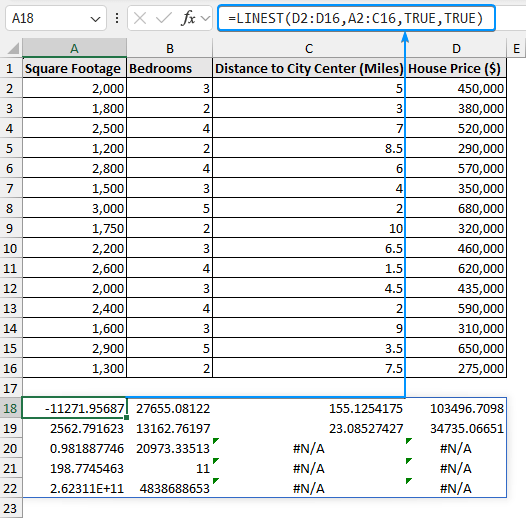
➤ In cell A18, enter the formula. For earlier versions of Excel press the Ctrl + Shift + Enter keys. In newer versions, just press Enter .
=LINEST(D2:D16,A2:C16,TRUE,TRUE)
The regression equation is the same as before:
House price = 103,496.71 + 155.13 * Square footage + 27,655.08 * Bedrooms - 11,271.96 * Distance to city center
➤ The standard error for the distance to the city center is 2562.79.
➤ The standard error for the bedrooms is 13162.76.
➤ The standard error for the square footage is 23.09.
➤ The standard error for the intercept is 34735.07.
➤ The R square is .9819.
➤ The residual standard error for y is 20973.34.
➤ The overall F statistic is 19877.
➤ The degree of freedom is 11.
➤ The regression sum of squares is 2.62E+11.
➤ The residual sum of squares is 4838688653.
Frequently Asked Questions
How do you run a multiple linear regression in Excel?
Select data >> Data tab >> Data Analysis >> Regression >> Input Y range >> Input X ranges >> Labels >> Output range >> OK.
Or,
=LINEST(known_ys,[known_xs],[const],[stats])
When to use multiple linear regression?
Multiple linear regression should be used when there are multiple independent variables and one dependent variable.
How can I interpret the regression output in Excel?
Key metrics:
- R squared: A value of 1 means the model perfectly explains all the variability while 0 indicates no relationship.
- P value: Check the statistical significance. The model is reliable if the P value is less than the significance level.
Correlation coefficient: Indicates the strength and direction.
What is the Adjusted R squared value?
Adjusted R squared adjusts the R squared value for the number of independent variables in the model, making it more reliable for models with multiple independent variables.
Wrapping Up
In this tutorial, we’ve learned about multiple linear regression and how to do multiple linear regression in Excel using Data Analysis ToolPak and the LINEST function. Feel free to download the practice file and let us know which method you like the most.